The history of encryption goes back several millennia, and ciphers used to secretly exchange information have existed almost as long as written language itself. Perhaps the most well known early cipher is the Caesar cipher, said to have been used by Julius Caesar over 2000 years ago. This method of encryption is very simple, to encrypt the secret message one simply shifts every character in the alphabet by a fixed number of steps, wrapping around when passing the last letter. Anyone who knows the encryption rule as well as the length of the shift, known as the cryptographic key, can unlock the message an read it.
While this ancient cipher is exceedingly simple, it nevertheless illustrates two key features of cryptography. The first feature is that because there is a rule that was used to encrypt the message there will be some hidden structure in the. A method that a malicious third party might use to retrieve the original message is to study the frequency with which each character appears. In English, for example, the most frequently occurring character is “e”, followed by “t”.
The second feature of the cipher is that since the same key is used to encrypt and decrypt the message, and this type of cipher is an example of symmetric encryption. The two parties who want to exchange encrypted messages therefore need to share the secret key, otherwise the recipient of the message won’t be able to unscramble it. One can’t simply send the key to the recipient though, because there’s no way to guarantee that someone won’t read it along the way. Unless, of course, the key is encrypted. However, if the key is encrypted that means that the two parties already shared a key. This chicken and egg problem of how to share the key is known as the key exchange problem.
For almost the entire history of cryptography, the key exchange problem has been solved by two people physically meeting and exchanging a set of cryptographic keys. In World War II, for instance, the German military distributed codebooks that specified which cryptographic keys would be used together with their Enigma machines on a certain day.
Fast forward to 2023 and encryption is used everywhere in our daily lives, to secure financial transactions and the privacy of our data, without having to physically meet and exchange keys. All this was enabled by the discovery, in the mid 1970’s, of a form of encryption called public-private cryptography. This is a form of cryptography where a message is encrypted with a key called the public key, which can be known by anyone. To decrypt the message one needs access to the private key, which should only be known by the recipient.
A way to think about how this type of encryption works is that the public key is an open padlock that is handed out freely. Anyone can use such a padlock to lock - encrypt - their message, but only the recipient has the key, and is therefore the only one who can unlock the message. In this analogy, the padlock is a mathematical function that is easy to compute in one direction, but “hard” to compute in the other direction.
The currently most commonly used public-private encryption algorithm used on the internet is RSA, or Rivest–Shamir–Adleman after its investors. The padlock function for this algorithm has to do with the problem of factoring a large numbers into prime numbers: if one picks two large prime numbers, it is easy to multiply them together to get a much larger number; however, it turns out to be very hard to do the process in reverse, and figure out which two prime numbers were multiplied together to generate the larger number.
The larger the numbers the harder the problem, and implementations of RSA typically use numbers so large that they would take millions of years to factor on even our fastest computers, and this is where the security of the cipher comes from. If someone discovered a clever way to perform the factoring, then they could suddenly break most encryption on the internet.
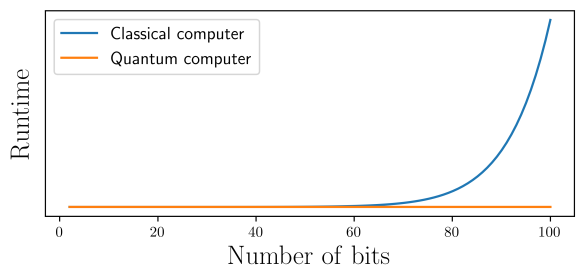
Computer scientist and cryptographers have had good reasons to think such a breakthrough isn’t possible, but this all changed in 1994 when the mathematician Peter Shor discovered a way to quickly factor large numbers using a quantum computer. The implications of this discovery were immediately understood, and led to a still ongoing multi-decadal effort to develop a useful quantum computer.
While quantum computers may in the future endanger cryptography on the internet, quantum mechanics also offers up a solution to the problem, specifically to the key exchange problem. This solution is known as quantum key distribution (QKD).
Quantum key distribution offers a way for two people to share a secret key in a way that cannot be intercepted by a malicious third party, and security of the key exchange does not rely on assumptions about the hardness of certain mathematical problem or the trust of a third party; instead, the security is based entirely in fundamental properties of quantum mechanics.
The conceptually most simple method, or protocol, for doing QKD was discovered by Charles Bennett and Gilles Brassard in 1984, and is therefore referred to simply as BB84. In this protocol, we imagine a scenario where one person, Alice, wants to share a key with another person Bob, without a third party, Eve, learning any information about the key. Alice does this by sending a string of single photons, each encoding a quantum state, to Bob.
The quantum states that Alices sends to BoB can be ‘up’, ‘down’, ‘left’, or ‘right’, but she doesn’t communicate which of these states she sends. When Bob receives a photon he measures its state. A measurement of a quantum system can be thought of as asking it a question, for example “are you up or down”, or “are you left or right”. There are two important things to understand how these questions work. The first is that if you ask a question that the quantum particle “doesn’t know” the answer to, then it will answer randomly. For example, if you ask a particle that is in the state ‘up’ whether it is ‘left’ or ‘right’ it will give either answer with 50% chance.
The second important thing is that when asking the same question twice in a row you will always get the same answer. Suppose the particle in the previous example answers ‘left’, and we once again ask it the same question, it will answer ‘left’ again. Since what it means for a particle to be in a certain state is that it gives the corresponding answer 100% of the time, this tells us that the particle now is ‘left’, and the act of asking the question has destroyed the information the particle initially was ‘left’. As we will see, it is these two facts that makes it impossible for Eve to gain information about the secret key without being detected.
Since Alice doesn’t tell Bob what state she prepared, Bob doesn’t know what questions to ask the photons he receives. Here will therefore ask each photon a random question. When he asks the right question the answer he gets will reveal which state Alice prepared, and when he asks the wrong question he will get a random answer. After all the photons from Alice have been received and measured by Bob, Alice will tell Bob what the right question for each photon was, and Bob will tell Alice what questions he asked. This communication can take place on an open channel, since it doesn’t reveal any information about what the actual answers were.
Alice and Bob now both know for which photons Bob got the answer that Alice prepared, and the corresponding set of answers is exactly the secret key.
What happens if Eve tries to listen in on the photons in order to intercept the key? To get information from the photons, Eve would have to measure them. Just like Bob, she doesn’t know what the right questions to ask are, and when she guesses wrong her measurements will change the quantum state. This in turn changes the answers that Bob get, and can therefore be detected.
To illustrate this, suppose that Alice once again prepares the state ‘up’, and Eve intercepts this photon, measures it ‘left’/‘right’ and gets the answer ‘right’. After the measurement the photon is then in the state ‘right’, and if Bob asks what would be the correct question, ‘up’/‘down’, he will get the wrong answer half of the time. If Alice and Bob take some part of their secret key and publicly announce it, they can check for errors, and the these errors would indicate the presence of an eavesdropper. If that is the case, Alice and Bob can no longer establish a shared key, and Eve’s actions constitute a denial of service attack, but no private information was compromised.
Quantum key distribution is one of the currently mature quantum technologies, with a multitude of companies offering QKD systems of various kinds. One of the challenges in deploying these systems is that the distance over which keys can be securely exchanged is limited. This is because when the single photons are transmitted in optical fibre there is a small probability that they will be lost. This can happen due to various physical processes, such as the photon hitting a small defect or simply being absorbed. The probability of the photon arriving successfully decreases exponentially with the distance between Alice and Bob. In classical optical networks, such as the ones used to transmit this blog to you, this problem is overcome by amplifiers that periodically boost the signal. This isn’t possible for the single photon quantum states: if it were then Eve could amplify the state, measure one part of it, and pass the rest on to Bob.
At the moment, QKD is therefore most suitable for intracity networks, or intercity links between cities that are reasonably close together. SURF is currently involved in setting up a testbed for such a network, as part of the European Quantum Communication Infrastructure Initiative, but more about that at a later date!



0 Praat mee